Узнайте о происхождении и значимости теоремы Пифагора, которая определяет соотношение между сторонами прямоугольного треугольника. Изучите различные способы ее доказательства и практическое применение в геометрии и физике.
Cодержание
Теорема Пифагора – одна из наиболее известных и значимых теорем в геометрии. Она устанавливает соотношение между сторонами прямоугольного треугольника. Сумма квадратов катетов равна квадрату гипотенузы: a^2 + b^2 = c^2. Названа в честь древнегреческого ученого Пифагора, который внес огромный вклад в развитие различных сфер античного мира.

Кто такой Пифагор?
Пифагор был древнегреческим философом и ученым, известным своими трудами в математике, физике, музыке, и других областях. Он является одним из наиболее значимых ученых Древней Греции и считается основателем пифагорейского братства. Доказательство закономерности соотношения сторон прямоугольного треугольника стало одним из его наиболее известных достижений.
Как была выведена теорема Пифагора?
Существуют различные версии о том, как была выведена теорема Пифагора. Одна из классических версий рассказывает о том, что Пифагор нарисовал на песке три квадрата, где каждая сторона квадрата стала стороной треугольника. При осознании этого открытия, Пифагор отпраздновал его огромным пиром, на который пришлось заклать 100 быков. Однако, эти события были описаны древнегреческими историками после смерти Пифагора и некоторые современные исследователи сомневаются в их достоверности.
Существуют также другие предположения о том, что теорема Пифагора была известна не только древним грекам, но и другим древним цивилизациям, таким как китайцы и египтяне. Однако, благодаря популярности трудов ученых Эллады, доказательство теоремы Пифагора традиционно приписывается Пифагору.
См. также
Как это работает на практике?
Теорема Пифагора имеет применение в различных областях, особенно в геометрии и физике. Она позволяет нам определить длину третьей стороны прямоугольного треугольника, если известны длины двух других сторон. Формула теоремы Пифагора (a^2 + b^2 = c^2) широко используется при решении задач, связанных с треугольниками.
Теорема Пифагора была доказана множеством способов. В научной литературе зафиксировано не менее 400 доказательств данной теоремы. Основные направления доказательств включают алгебраическое использование соотношений элементов треугольника, метод площадей и различные экзотические методы, такие как использование дифференциальных уравнений.
Алгебраическое доказательство
Одним из наиболее популярных способов доказательства теоремы Пифагора является алгебраическое доказательство с использованием подобия треугольников. При этом используется свойство подобия треугольников с равными углами.
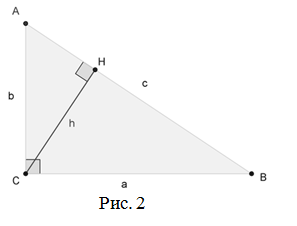
Для прямоугольного треугольника ABC с прямым углом при вершине C проводится высота CH, которая является основанием прямоугольного треугольника ACH. С помощью свойств подобия треугольников можно установить соотношения между сторонами треугольников ABC и ACH. Из подобия треугольников следует, что a/c = c/b, b/c = c/a. При перемножении этих пропорций получаем a^2 + b^2 = c^2, что является формулировкой теоремы Пифагора.
Доказательство методом площадей
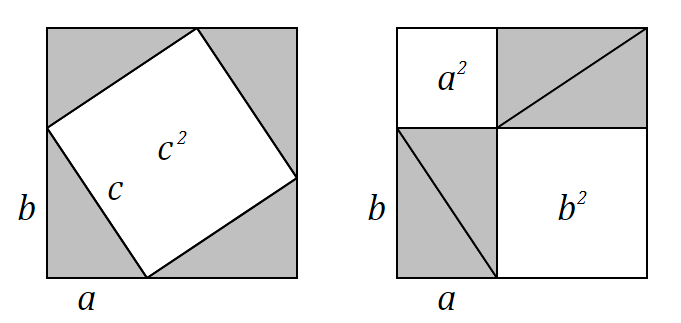
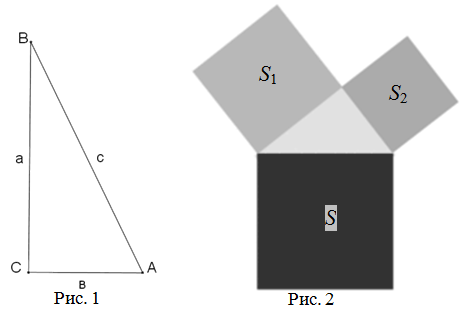
Множество доказательств теоремы Пифагора используют понятие площадей фигур. Идея основана на сравнении площадей квадратов, построенных на сторонах прямоугольного треугольника.
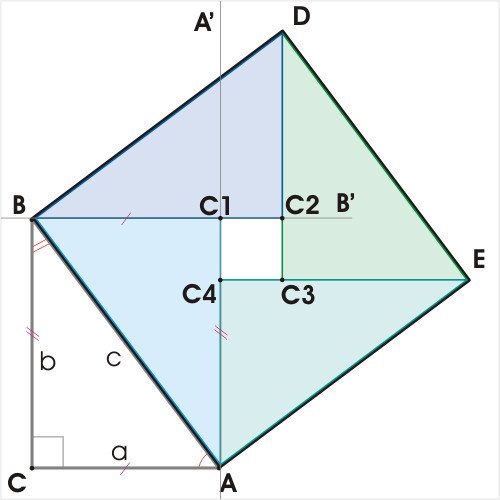
Пусть треугольник ABC является прямоугольным, где стороны a и b являются катетами, а сторона c – гипотенузой. Построим квадраты на сторонах треугольника: квадрат ACHB на стороне c, квадрат AFDE на стороне a и квадрат CGBF на стороне b. Площадь квадрата ACHB равна сумме площадей квадратов AFDE и CGBF. Таким образом, получаем a^2 + b^2 = c^2, что является теоремой Пифагора.

Историческая справка
История теоремы Пифагора насчитывает множество версий и предположений о ее происхождении. Уже в древнекитайской книге "Чжоу би суань цзин" говорится о пифагоровом треугольнике со сторонами 3, 4 и 5. Немецкий историк математики Мориц Кантор считает, что равенство 3^2 + 4^2 = 5^2 было известно египтянам еще около 2300 г. до н.э. В настоящее время в научной литературе зафиксировано более 367 доказательств теоремы Пифагора.
![Прелесть математики] Теорема Пифагора](https://blog.bc-pf.org/content/images/2021/02/pif2-1.png)
Заключение
Теорема Пифагора является одной из фундаментальных теорем в геометрии, которая имеет широкое практическое применение. Она была доказана множеством способов и продолжает быть предметом изучения и исследования для математиков всего мира. История ее происхождения окутана тайной и легендами, но ее значение и значимость несомненны.
См. также
Что нам скажет Википедия?
Также может быть выражена как геометрический факт о том, что площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах. Верно и обратное утверждение: треугольник, у которого сумма квадратов длин двух сторон равна квадрату длины третьей стороны, является прямоугольным.
Обратная теорема Пифагора — утверждение о прямоугольности всякого треугольника, длины сторон которого связаны соотношением a^2 + b^2 = c^2. Как следствие, для всякой тройки положительных чисел a, b и c, такой, что a^2 + b^2 = c^2, существует прямоугольный треугольник с катетами a и b и гипотенузой c. Предложение, обратное теореме Пифагора, сформулированное в условной форме: «Если квадрат одной из сторон треугольника равен сумме квадратов двух других сторон, то угол, лежащий против этой стороны, является прямым». Это же предложение в категоричной форме: «Угол треугольника, лежащий против стороны, квадрат которой равен сумме квадратов двух других сторон, прямой». Именно данное корректное предложение, обратное теореме Пифагора, является также теоремой.
В научной литературе зафиксировано не менее 400 доказательств теоремы Пифагора, что объясняется как фундаментальным значением для геометрии, так и элементарностью результата. Основные направления доказательств: алгебраическое использование соотношений элементов треугольника (таков, например, популярный метод подобия), метод площадей, существуют также различные экзотические доказательства (например, с помощью дифференциальных уравнений).
Через подобные треугольники: Одним из наиболее популярных в учебной литературе доказательств алгебраической формулировки является доказательство с использованием техники подобия треугольников, при этом оно почти непосредственно выводится из аксиом и не задействует понятие площади фигуры. В нём для треугольника △ABC с прямым углом при вершине C со сторонами a, b, c, противолежащими вершинам A, B, C соответственно, проводится высота CH, при этом (согласно признаку подобия по равенству двух углов) возникают соотношения подобия: △ABC∼△ACH и △ABC∼△CBH, из чего непосредственно следуют соотношения: a/c = c/b, b/c = c/a. При перемножении крайних членов пропорций выводятся равенства: a^2 + b^2 = c^2.
Доказательства методом площадей: Большое число доказательств задействуют понятие площади. Несмотря на видимую простоту многих из них, такие доказательства используют свойства площадей фигур, доказательства которых сложнее доказательства самой теоремы Пифагора.
Доказательство через равнодополняемость: Доказательство через равнодополняемость использует четыре копии прямоугольного треугольника с катетами a, b и гипотенузой c, расположенные таким образом, чтобы образовывать квадрат со стороной a + b и внутренний четырёхугольник со сторонами длиной c. Внутренний четырёхугольник в этой конфигурации является квадратом, так как сумма двух противоположных прямому острых углов — 90°, а развёрнутый угол — 180°. Площадь внешнего квадрата равна (a + b)^2, он состоит из внутреннего квадрата площадью c^2 и четырёх прямоугольных треугольников, каждый площадью ab/2, в результате из соотношения (a + b)^2 = 4(ab/2) + c^2 при алгебраическом преобразовании следует утверждение теоремы.
Доказательство Евклида: Классическое доказательство Евклида направлено на установление равенства площадей между прямоугольниками, образованными из рассечения квадрата над гипотенузой высотой из прямого угла с квадратами над катетами.



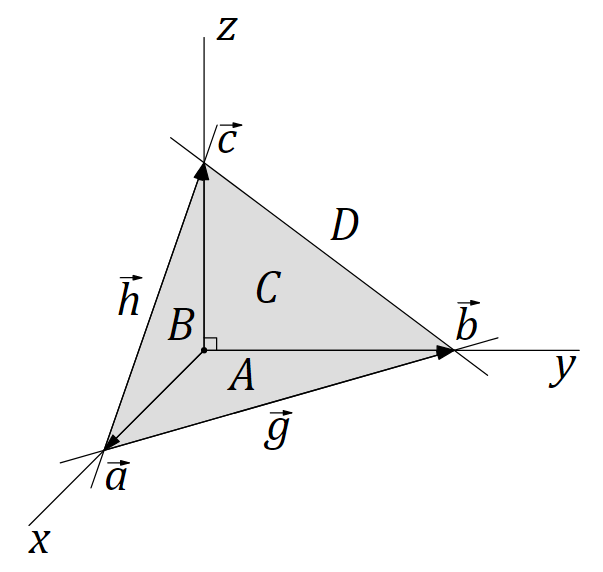

![Прелесть математики] Теорема Пифагора](https://blog.bc-pf.org/content/images/2021/02/pif3-1.png)