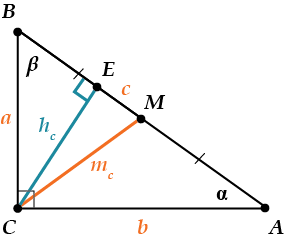Узнайте о связи между Пифагором и прямоугольным треугольником, включая теорему Пифагора, обратную теорему Пифагора и использование Пифагоровых троек. Изучите особые треугольники в математике - золотой и серебряный треугольники.
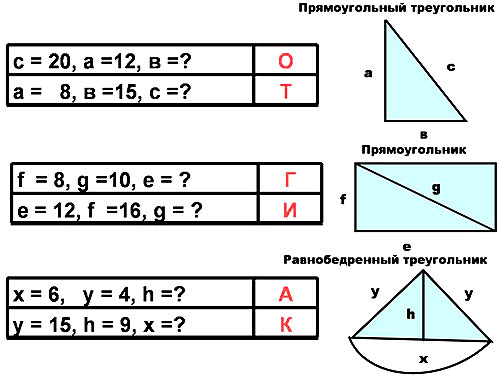
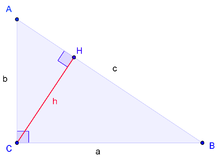
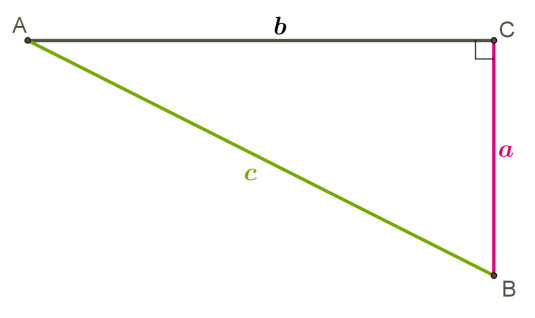
Прямоугольный треугольник – это треугольник, у которого один угол равен 90°. Сторона, лежащая против такого угла, называется гипотенузой (с), а две другие стороны – катетами (a и b).
Теорема Пифагора
Одной из самых известных математических теорем, связывающих прямоугольный треугольник и Пифагора, является теорема Пифагора. Она утверждает, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов:
AB² = AC² + CB²
Теорема Пифагора доказывает важное свойство прямоугольных треугольников и является основой для многих геометрических и тригонометрических выкладок.
Обратная теорема Пифагора
Обратная теорема Пифагора утверждает, что если для сторон произвольного треугольника выполняется условие AB² = AC² + CB², то такой треугольник является прямоугольным. Это позволяет использовать теорему Пифагора для определения прямоугольности треугольника по его сторонам.
Пифагоровы тройки
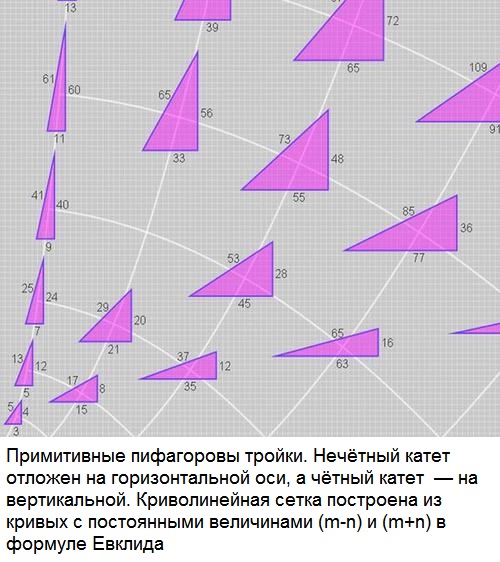
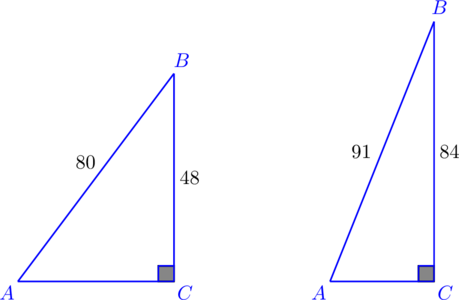
При работе с прямоугольными треугольниками часто используются так называемые Пифагоровы тройки. Пифагоровы тройки – это наборы трех целых чисел (a, b, c), удовлетворяющие теореме Пифагора. То есть, если a, b и c образуют Пифагорову тройку, то выполняется равенство:
a² + b² = c²
Например, Пифагоровы тройки могут быть следующими: (3, 4, 5), (5, 12, 13), (7, 24, 25) и т.д. Для Пифагоровых троек также существуют особые свойства и отношения между сторонами треугольника.
Особые треугольники
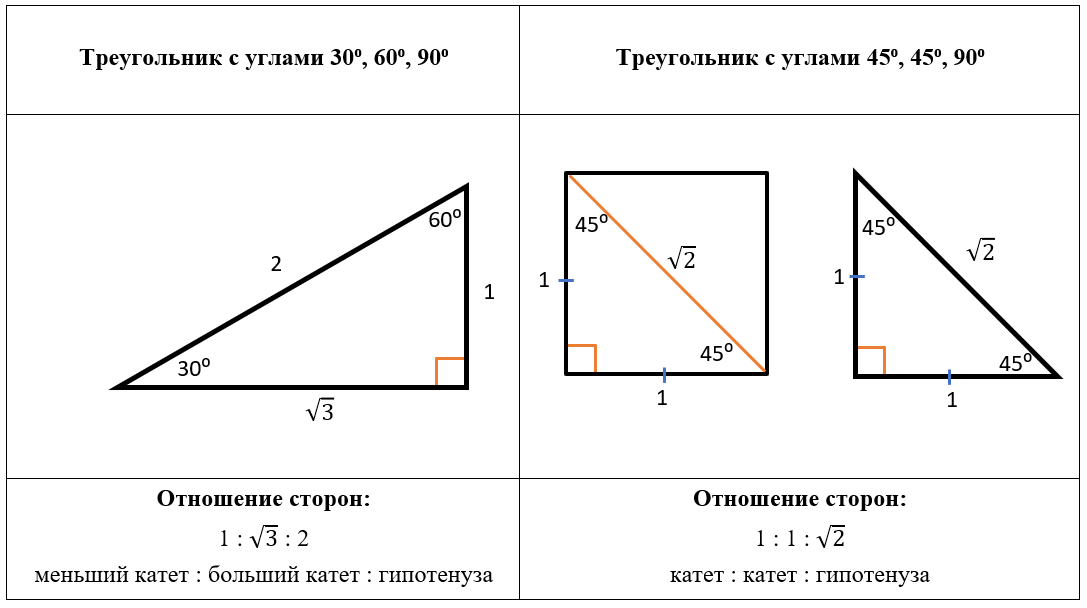
В математике выделяются два особых треугольника, в которых отношения сторон сохраняются и часто используются:
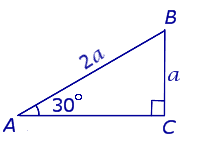
1. Золотой треугольник: в треугольнике с углами 30°, 60° и 90° катет, лежащий против угла в 30°, равен половине гипотенузы. Если один катет равен а, то гипотенуза равна 2а, а второй катет можно посчитать по теореме Пифагора.
2. Серебряный треугольник: в треугольнике с углами 45°, 45° и 90° оба катета равны. Такой треугольник является равнобедренным, и его гипотенуза можно посчитать по теореме Пифагора.
Используя эти особые треугольники, можно легко вычислять отношения сторон и проводить геометрические расчеты.