В данной статье мы рассмотрим различные методы и формулы для вычисления катета в прямоугольном треугольнике восьмого класса. Одним из основных способов нахождения катета в прямоугольном треугольнике является использование теоремы Пифагора. Вычисление катета по теореме Пифагора, вычисление катета с использованием тригонометрических функций острых углов, заключение.
Cодержание
В данной статье мы рассмотрим различные методы и формулы для вычисления катета в прямоугольном треугольнике восьмого класса.
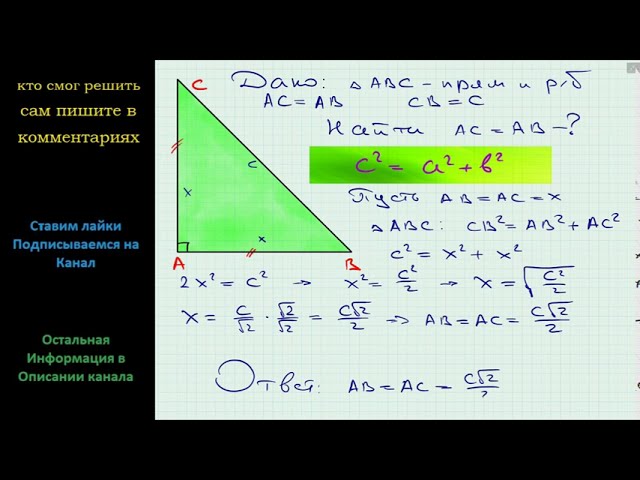
Теорема Пифагора
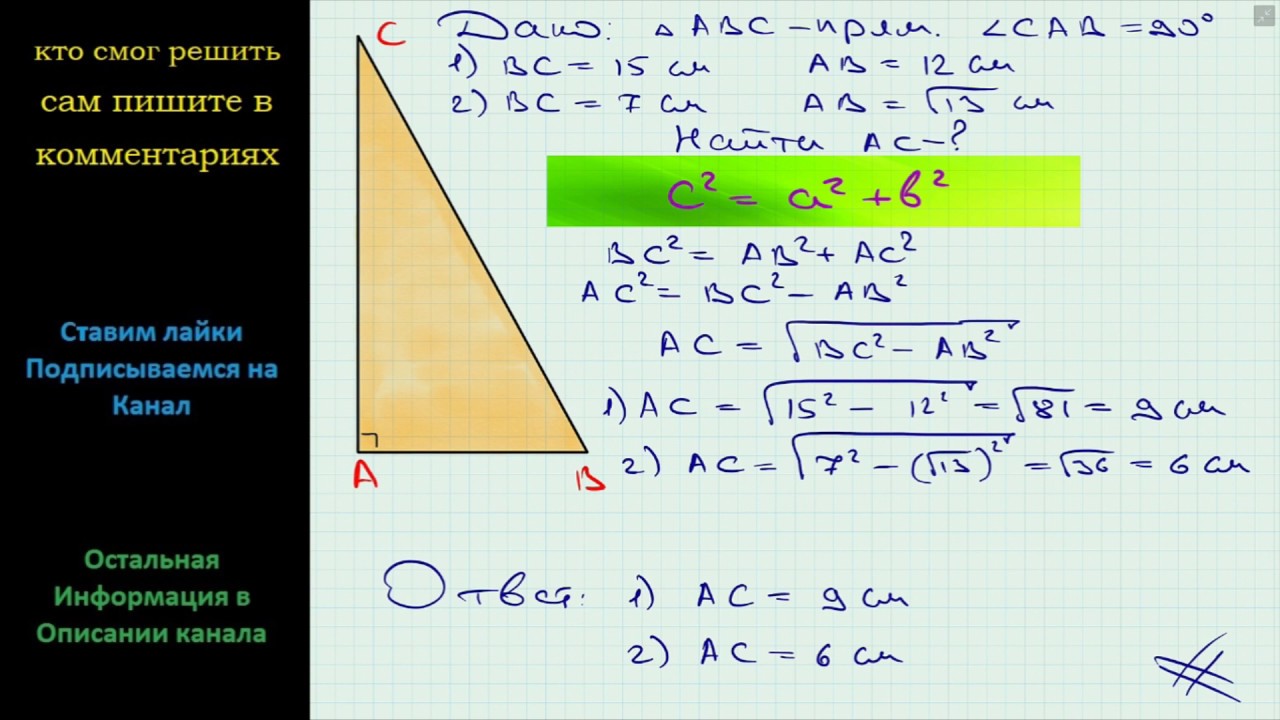
Одним из основных способов нахождения катета в прямоугольном треугольнике является использование теоремы Пифагора. Согласно этой теореме, квадрат гипотенузы равен сумме квадратов катетов:
AB^2 = AC^2 + BC^2
Вычисление катета по теореме Пифагора
Если в прямоугольном треугольнике известны один катет и гипотенуза, то длину второго катета можно вычислить по теореме Пифагора. Формула для вычисления второго катета выглядит следующим образом:
b = √(c^2 - a^2)
Например, если гипотенуза (c) равна 9, а один катет (a) равен 6, то второй катет (b) будет равен:
b = √(9^2 - 6^2) = √(81 - 36) = √45 ≈ 6,71
Таким образом, второй катет равен примерно 6,71.
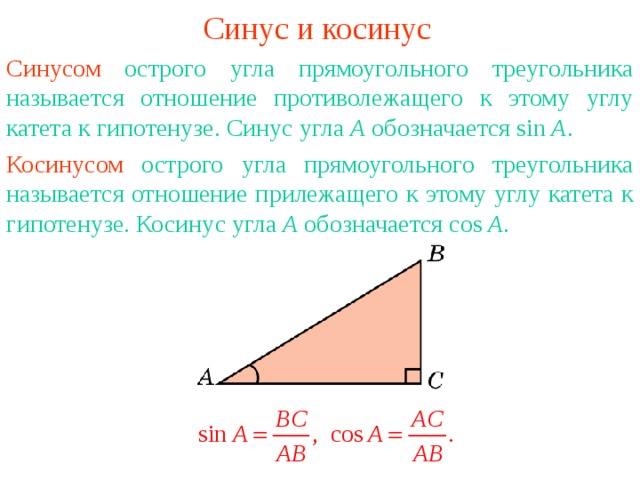
Тригонометрические функции в прямоугольном треугольнике
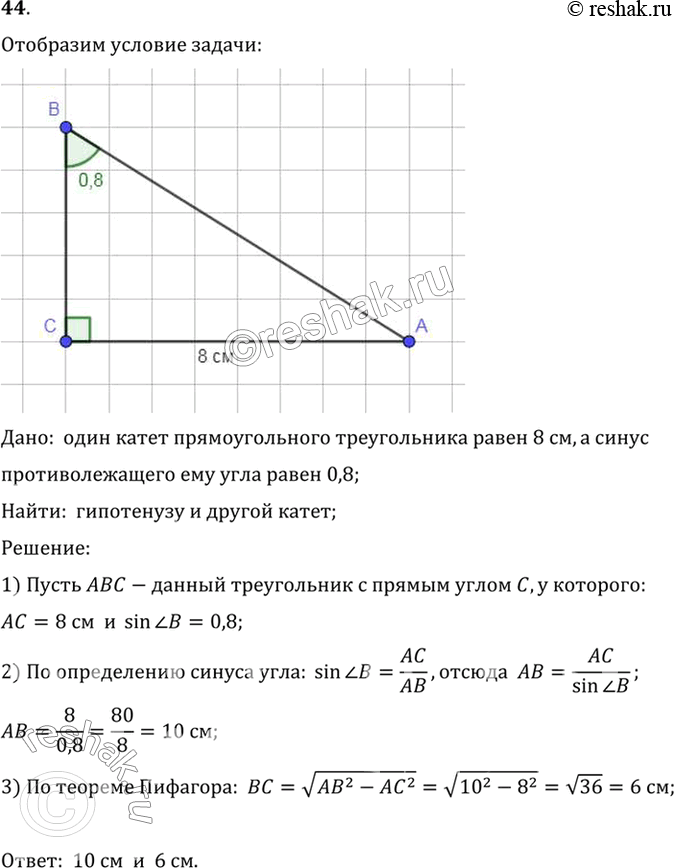
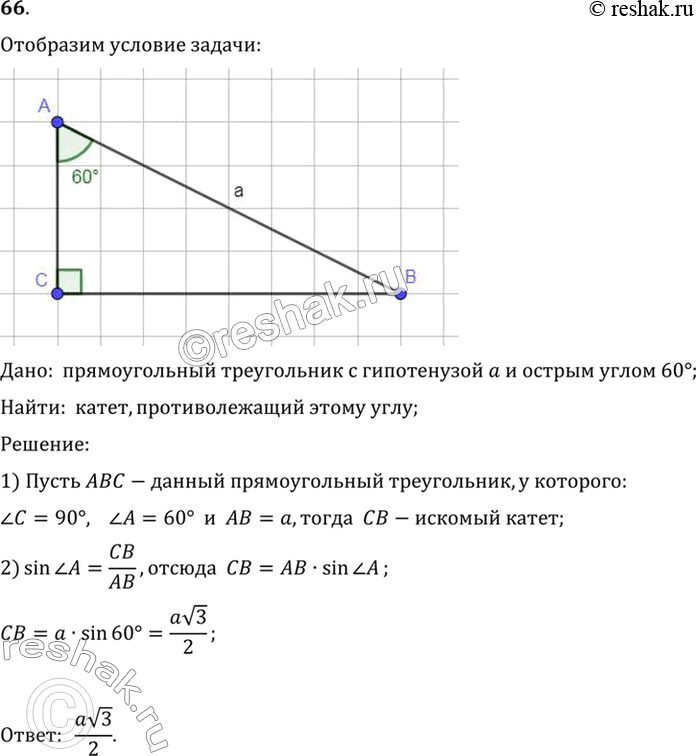
Для вычисления катета в прямоугольном треугольнике также можно использовать тригонометрические функции острых углов. В прямоугольном треугольнике определяются следующие тригонометрические функции:
- Синус угла (sin) - отношение противолежащего катета к гипотенузе: sin(α) = a/c
- Косинус угла (cos) - отношение прилежащего катета к гипотенузе: cos(α) = b/c
- Тангенс угла (tg) - отношение противолежащего катета к прилежащему: tg(α) = a/b
- Котангенс угла (ctg) - отношение прилежащего катета к противолежащему: ctg(α) = b/a
Используя соответствующую формулу для тригонометрической функции, можно выразить катет через гипотенузу и синус (или косинус) острого угла.
Заключение
В данной статье мы рассмотрели различные методы и формулы для вычисления катета в прямоугольном треугольнике. Одним из основных способов является использование теоремы Пифагора, а также вычисление катета с использованием тригонометрических функций острых углов. Зная длину гипотенузы и одного катета, можно легко вычислить длину второго катета, что делает эти методы очень полезными при решении задач на поиск катета в прямоугольном треугольнике.