Почему 8 не является простым числом?

Узнайте, почему число 8 не является простым числом и как основная теорема арифметики и история изменили определение простых чисел.

Простое число — натуральное число, имеющее ровно два различных натуральных делителя. Другими словами, натуральное число p является простым, если оно отлично от 1 и делится без остатка только на 1 и на само p.

Пример: число 2 простое (делится на 1 и на 2), а 4 не является простым, так как, помимо 1 и 4, делится на 2 — имеет три натуральных делителя.

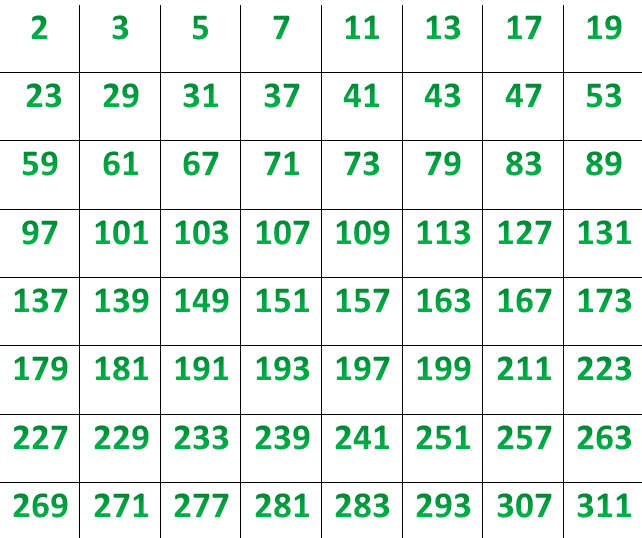
Натуральные числа можно разделить на три класса: единица (имеет один натуральный делитель), простое число (имеет два натуральных делителя), составное число (имеет более двух натуральных делителей). Как простых, так и составных чисел бесконечно много.

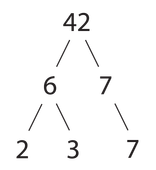
Основная теорема арифметики устанавливает, что каждое натуральное число, большее единицы, представимо в виде произведения простых чисел, причём единственным способом с точностью до порядка следования сомножителей. Таким образом, простые числа являются элементарными «строительными блоками» натуральных чисел.

Историческая справка

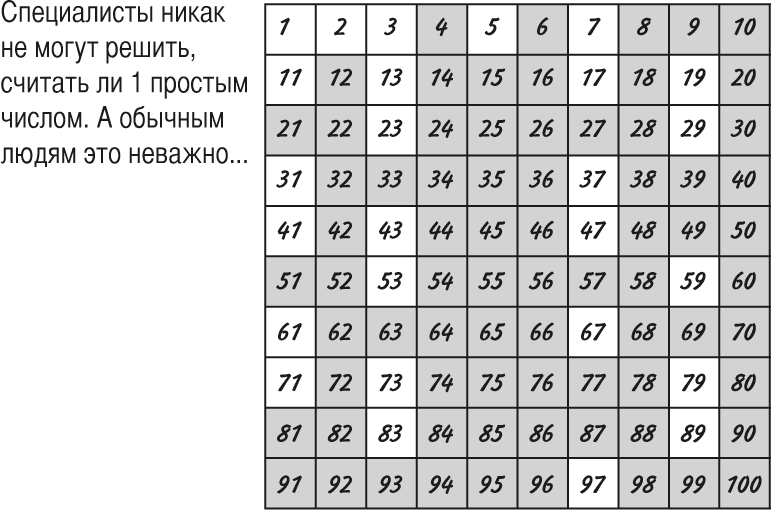
Большинство древних греков даже не считало 1 числом, поэтому они не могли считать его простым. К Средним векам и эпохе Возрождения многие математики включали 1 в качестве первого простого числа. В середине XVIII века Христиан Гольдбах внёс в список 1 в качестве первого простого числа в своей знаменитой переписке с Леонардом Эйлером; однако сам Эйлер не считал 1 простым числом. В XIX веке многие математики по-прежнему считали число 1 простым числом.

Моё математическое образование научило меня, что хорошей причиной того, почему 1 не считается простым, является основная теорема арифметики. Она утверждает, что каждое число может быть записано как произведение простых чисел ровно одним способом. Если бы 1 было простым, мы бы потеряли эту уникальность. Мы могли бы записать 2 как 1×2, или 1×1×2, или 1×2. Исключение 1 из простых чисел устраняет это.

Изначально я планировала в статье объяснить основную теорему арифметики и покончить с этим. Но на самом деле не так сложно изменить формулировку теоремы для решения проблемы с единицей. В конце концов, вопрос моего друга разжёг моё любопытство: как математики остановились на этом определении простого числа? Беглый поиск показал, что единица раньше считалась простым числом, а сейчас нет. Но статья Криса Колдуэлла и Енг Сюна демонстрирует немного более сложную историю.

Колдуэлл и Сюн начинают с классических греческих математиков. Они не считали 1 числом так же, как 2, 3, 4 и так далее. 1 считалась цифрой, а число состояло из нескольких цифр. По этой причине 1 не могла быть простым — это даже не число. Арабский математик IX века аль-Кинди писал, что это не число и, следовательно, не является чётным или нечётным. В течение многих веков преобладало представление, что единица — это строительный блок для составления всех чисел, но не само число.

В 1585 году фламандский математик Симон Стивин в своей работе «Аритметическое учение» утверждал, что 1 не является ни простым, ни составным. Он ввёл термини унита (лат. unitas), чтобы отличить его от простых и составных чисел. Он также ввёл термин декада (лат. decada) для обозначения числа 10. Таким образом, 1 была представлена в качестве особого типа числа, отличного от простых и составных.

С увеличением знаний о числах и их свойствах, математики стали стремиться к более четкому и конкретному определению простого числа. Идея о двух различных делителях стала доминирующей, что привело к исключению 1 из простых чисел.

Таким образом, в современной математике 8 не является простым числом, так как оно имеет более двух натуральных делителей (1, 2, 4 и 8).

Вывод

Исключение числа 1 из простых чисел обусловлено основной теоремой арифметики и постепенным изменением определения простого числа со временем. Современное определение простого числа требует наличия ровно двух различных натуральных делителей, что исключает 1 из этой категории чисел. Таким образом, 8 не является простым числом, так как оно имеет более двух натуральных делителей.

Что нам скажет Википедия?

Простое число — натуральное число, имеющее ровно два различных натуральных делителя. Другими словами, натуральное число p является простым, если оно отлично от 1 и делится без остатка только на 1 и на само p.

Пример: число 2 простое (делится на 1 и на 2), а 4 не является простым, так как, помимо 1 и 4, делится на 2 — имеет три натуральных делителя.

Натуральные числа можно разделить на три класса: единица (имеет один натуральный делитель), простое число (имеет два натуральных делителя), составное число (имеет более двух натуральных делителей). Как простых, так и составных чисел бесконечно много.

Основная теорема арифметики устанавливает, что каждое натуральное число, большее единицы, представимо в виде произведения простых чисел, причём единственным способом с точностью до порядка следования сомножителей. Таким образом, простые числа являются элементарными «строительными блоками» натуральных чисел.

Большинство древних греков даже не считало 1 числом, поэтому они не могли считать его простым. К Средним векам и эпохе Возрождения многие математики включали 1 в качестве первого простого числа. В середине XVIII века Христиан Гольдбах внёс в список 1 в качестве первого простого числа в своей знаменитой переписке с Леонардом Эйлером; однако сам Эйлер не считал 1 простым числом. В XIX веке многие математики по-прежнему считали число 1 простым числом.